Is Currying in JavaScript, A Chain of Functions?

In this article, we are going to discuss “Is Currying in JavaScript a Chain of Functions?“. Here, we will see how currying works like a chain of functions and how it will be useful for developers. We will also see the conversion of an existing function into the current version. Let’s start our topic, i.e., Is Currying in JavaScript a Chain of Functions?

Yes, Currying in JavaScript is a chain of functions. Currying is an advanced technique commonly used in functional programming that allows you to transform a function with multiple arguments into a sequence of functions, each taking only one argument at a time.

log(a,b,c) => log(a)(b)(c)

A functional programming technique involves breaking down a function that takes multiple arguments into a series of smaller functions, each taking one argument. This creates a chain of functions, where each function returns another function until the final result is achieved.

Currying in JavaScript is named after the mathematician Haskell Curry, who introduced it in the 1930s. Some say that currying calls a function, but it doesn’t. Currying doesn’t call a function. It just transforms it. It’s also used in other languages as well. Let’s start with the code, later on, will be discussing the advantages.

Starting with the standard example of an addition/sum function,

Converting it into a currying function,

In this curried version of the addition function, each function takes one argument and returns another function until all the arguments are collected and the final sum is calculated.

Here’s how the currying works step by step:

1. addition(1) returns a function that takes the second number.
2. addition(1)(2) / sumResult1(3) returns a function that takes the third number.
3. addition(1)(2)(3) returns the final result, which is the sum of all three numbers.

This way, you can call the curried addition function with each argument separately, creating a more modular and composable function. We can reuse this function throughout our codebase without duplicating the logic. Another advantage of currying is the ability to create higher-order functions that enhance composability.

Infinite Currying?

Via using some of the recursive nature techniques, we can convert the function code to have an infinite argument. This allows you to create an infinite currying chain, where you can keep adding numbers as needed, and when you’re ready to get the final result, you just need to call the curried function with no arguments to compute the sum.

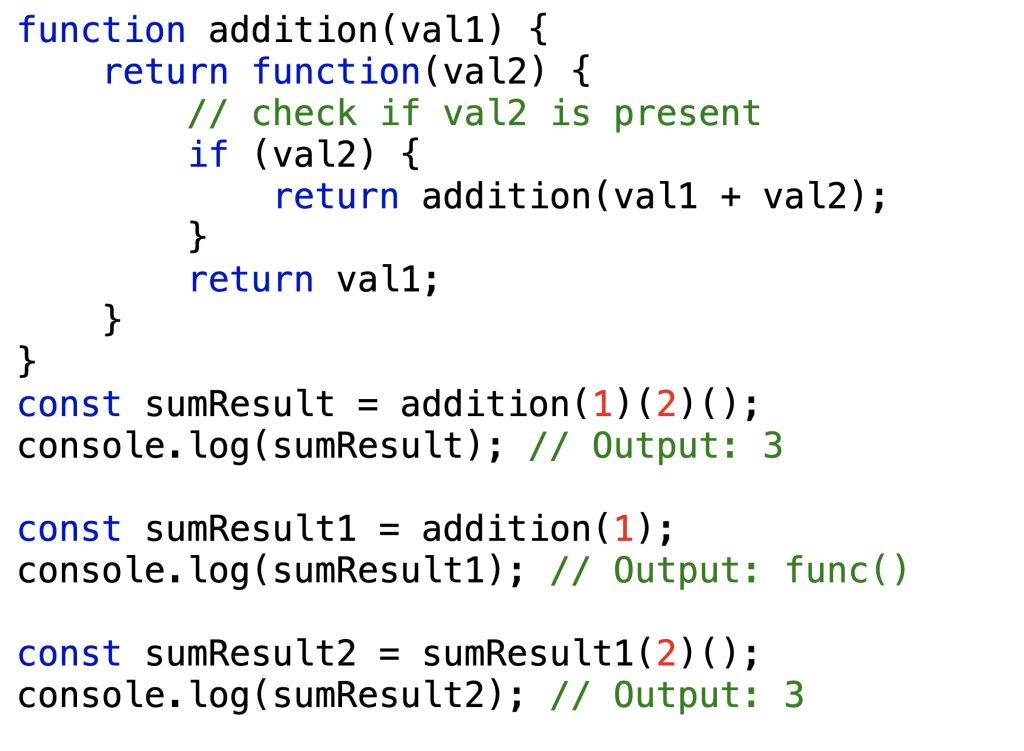
Let’s dry-run it:

1. The addition function is defined to accept a single argument val1.
2. Inside the addition function, an inner function is returned. This inner function takes an argument val2.
3. If val2 is provided (i.e., it’s truthy), the inner function returns a recursive call to addition with the sum of val1 and val2.
4. If val2 is not provided (i.e., it’s falsy, like undefined or 0), the inner function returns the accumulated val1.
5. When the curried addition function is called, it can be immediately invoked with the next argument, and this process can be repeated for as many arguments as needed.
6. The final invocation of the curried addition function is done with an empty set of parentheses (). This results in computing the accumulated sum of all previously provided numbers.
7. The result is 3, which is the sum of 1 and 2.

Summary

Currying is a transform that makes f(a,b,c) callable as f(a)(b)(c). JavaScript implementations usually keep the function callable normally and return the partial if the arguments count is insufficient.

Currying allows us to get the partials easily. As we’ve seen in the addition()  example, after currying the three arguments function addition(val1, val2, val3) gives us partials when called with one argument (like addition(val1)) or two arguments (like addition(val1, val2)).