Exploring Fundamental Sorting Algorithms in Computer Science
What is Sorting?

Sorting is a process of arranging data in specific orders, it can be based on some criteria such as numerical values, alphabetical order, or some other characteristics.
In computer science, sorting typically involves rearranging elements in an array, list, or other data structure so that they are in a predetermined sequence. This sequence could be ascending or descending for numerical values, or alphabetical for strings of text.
Sorting is not only important in computer science but also in various real-world applications. For example, sorting is used in databases to organize records, in e-commerce websites to display products in a specific order (Sorting Items based on price as Low-to-Hight, High-to-Low), in search engines to rank search results, and in many other scenarios where data needs to be organized for easy access and retrieval.
Sorting Terminology
Sorting terminology is like a special set of words we use to talk about how we organize things. It helps us describe how we sort data, like numbers or words, and how different ways of sorting work. Just like we have words to describe how we clean up a messy room, sorting terminology gives us the language to talk about how we tidy up our data.
Elements: Think of elements as items in a toy chest. Each toy — like a ball, doll, or car — is an element. So in programming elements can be numbers, strings, objects, or any other data type
Comparison: The act of evaluating two elements to determine their relative order. Sorting algorithms often rely on comparisons to arrange elements correctly. When you decide which toy is bigger or smaller, you’re comparing them. Sorting does this with numbers or words to figure out their order.

Key: The value used for comparison during sorting. For example, when sorting a list of objects by a specific attribute, that attribute serves as the key. Imagine you’re sorting a bunch of toys by their sizes. The size of each toy is like its key — it’s what you’re looking at to decide where it goes on the shelf.
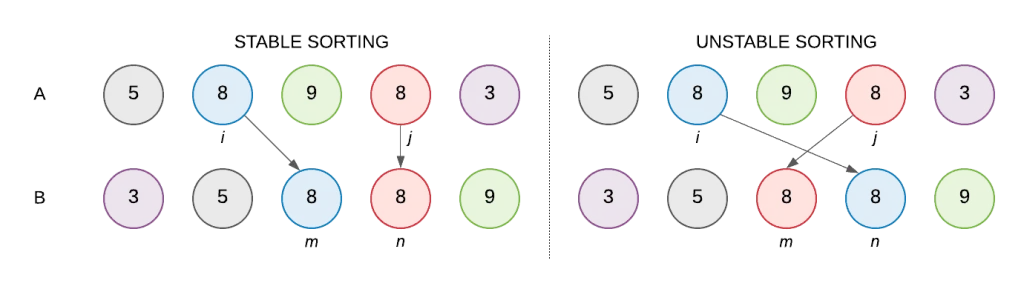
Stable Sorting: A sorting algorithm is stable if it preserves the relative order of equal elements. In other words, if two elements have the same value, their original order remains unchanged after sorting. Imagine you’re cleaning up your toys. You have a bunch of stuffed animals and you want to sort them by color. Now, let’s say you have two blue teddy bears. Stable sorting is like making sure those two blue teddy bears stay in the same order they were originally in when you finish sorting. So, even after you’ve organized all the toys by color, those two blue teddy bears will still be in the same order they were before you started sorting. It’s like keeping things in line, even after you’ve finished cleaning up.

Unstable Sorting: Unstable sorting is a type of sorting algorithm where elements with equal keys (values used for sorting) may change their relative order after sorting. In other words, if two elements have the same key, there’s no guarantee that they’ll maintain their original order in the sorted sequence. This can happen during certain operations within the sorting process, causing elements with equal keys to be rearranged unpredictably.
Imagine you have a line of toys, like cars, all lined up according to their colors. Now, if you want to sort them by size, unstable sorting means that sometimes when you’re arranging the toys, two toys of the same color might end up switching places unexpectedly. So, after you finish sorting, the order of those toys with the same color might not be the same as it was at the beginning.
In-Place Sorting: An in-place sorting algorithm sorts the elements within the original data structure without requiring additional memory space proportional to the size of the input. This is desirable for sorting large datasets with limited memory resources. Sorting your toys without using any extra baskets or boxes is like doing it “in-place.” You’re just rearranging them without needing more space.

Adaptive Sorting: An adaptive sorting algorithm is one that becomes more efficient when dealing with partially sorted data. It can recognize and take advantage of existing order in the data to improve performance. Let’s say you’re sorting your toys, and suddenly you realize some are already in order by color. An adaptive sorter can recognize that and finish quicker.
Time Complexity: The measure of how the running time of an algorithm increases with the size of the input. Sorting algorithms are often analyzed in terms of their time complexity, typically expressed using Big O notation.
Time complexity is like figuring out how much time it will take to do something but for algorithms. When we talk about time complexity in computer science, we’re looking at how the time it takes for an algorithm to run increases as the size of the input data increases. It’s a way of understanding how efficient an algorithm is.
For example, let’s say you have a list of numbers, and you want to find the largest number in that list. If you use a simple algorithm that checks each number one by one, the time it takes will increase linearly with the size of the list. This is called linear time complexity and is often represented as O(n), where n is the size of the input.
Imagine you have a bunch of toys to tidy up. If you have only a few toys, it’s quick and easy to clean them up. But if you have a lot of toys, it might take longer. Time complexity helps us understand how long it will take for different ways of cleaning up toys.
Some ways of cleaning up toys might take longer as you have more toys, like checking each toy one by one. This is like linear time complexity — the more toys you have, the longer it takes.
But there are other ways of cleaning up toys, like if you sort them into piles based on their colors. This might take longer at first, but once you’ve sorted them, finding a specific color is much quicker. This is like logarithmic time complexity — even if you have more toys, it doesn’t take as much longer to find what you need

Space Complexity: The amount of additional memory space required by an algorithm to perform its task, relative to the size of the input.
Imagine you have a bunch of toys, and you need to sort them into different boxes. If you have only a few toys, you might not need many boxes, so the space you need is small. But if you have a lot of toys, you might need more boxes, which means you need more space.
Similarly, space complexity tells us how much extra memory an algorithm needs to do its job as the size of the input data increases. Some algorithms need a lot of extra memory, like if they make copies of the data, while others don’t need much extra space at all.
Understanding space complexity helps us choose the best algorithm for a task, especially when memory is limited or expensive. We want to use algorithms that are efficient with memory and don’t require more space than necessary to get the job done.

Worst-case, Best-case, and Average-case Complexity: Sorting algorithms may have different time complexities depending on the characteristics of the input data. The worst-case complexity represents the maximum time required for any input, the best-case complexity represents the minimum time required for a specific input, and the average-case complexity represents the expected time over all possible inputs.
- Worst-case scenario: Imagine you’re in a big room full of people, and you need to find someone who has a blue pen. In the worst-case scenario, you have to ask every single person in the room if they have a blue pen. This takes the longest time because you have to talk to everyone before finding the person with the blue pen.
- Best-case scenario: Now, in the best-case scenario, you walk into the room, and the first person you ask happens to have a blue pen. You find the blue pen right away without needing to ask anyone else. This is the shortest amount of time it takes to find the blue pen.
- Average-case scenario: In the average-case scenario, you have to ask a few people before finding someone with a blue pen. Some people might have it, some might not, but overall, it’s a moderate amount of effort and time to find the blue pen.
These scenarios illustrate how the time it takes to find the person with the blue pen can vary depending on different situations. Similarly, in computer science, we use worst-case, best-case, and average-case scenarios to understand how algorithms perform in different situations.
Sorting algorithms are the building blocks of efficient data organization in computer science, empowering developers to create streamlined and optimized solutions. Embrace these fundamental concepts to unlock the true potential of your programming journey.
Keep Learning! Keep Coding!

